Analytical modeling of wind-farms
Large eddy simulations of wind-farms are computationally very demanding and require the access to supercomputers to calculate the wind farm performance. The wind energy industry relies on simpler, much less computationally expensive, models to improve wind-farm design, as many scenarios need to be considered. Two common modeling approaches are wake models and the top-down model. Wake models approximate the growth of velocity deficits behind each turbine as linear and account for wake-wake interactions through superposition of squared velocity deficits. This approach captures the entrance effects well, but is less accurate in modeling the deep-array effects. "Top-down" models are able to capture the coupling between the wind-farm and the atmospheric boundary layer, but do capture the effects of relative turbine positioning.
Based on the insight obtained from our Large eddy simulations of wind-farms page we have recently developed the Coupled Wake Boundary Layer (CWBL) model, which proposes a two-way coupling between the Jensen wake model and the Calaf et al. "Top-down" model. A conceptual sketch of the coupling between the wake and the "top-down" model is given in figure 1. The "top-down" part of the CWBL models captures the deep farm effects and is used, via iterations, to determine the wake expansion coefficient needed in the wake model in order to accurately capture the fully developed regime of the wind-farm. Conversely, the "top-down" model requires specification of the effective wake area coverage, which depends on the turbine positioning and is determined with the wake model. Convergence to a consistent CWBL system is obtained by iterating until the mean streamwise velocity at turbine hub-height is the same in both models for the fully developed region of the wind-farm. The CWBL odel predictions are compared with field measurements and large eddy simulation results and the CWBL model is shown to provide improved predictions with respect a wake model further downstream in the wind-farm. Figure 2 shows an application of this model to the Horns Rev wind-farm in Denmark.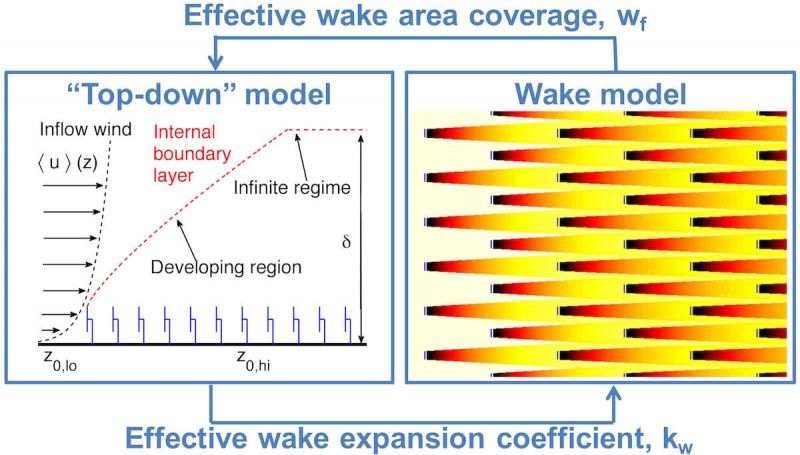
Figure 1: Conceptual sketch of the coupling between the wake and the "top-down" model. The "top-down" part captures the deep farm effects and is used, via iterations, to determine the wake expansion coefficient needed in the wake model in order to accurately capture the fully developed regime of the wind-farm. Conversely, the "top-down" model requires specification of an effective spanwise spacing. This distance depends on the turbine positioning and is determined with the wake model. Convergence to a consistent CWBL system is obtained by iterating until the mean streamwise velocity at turbine hub-height is the same in both models for the fully developed region of the wind-farm.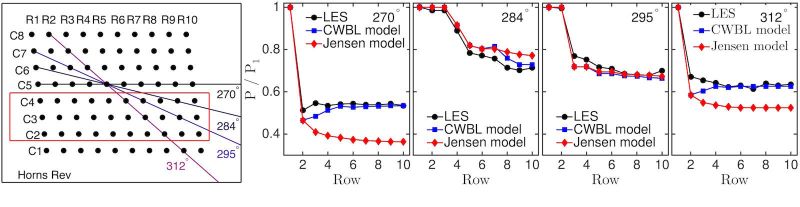
Figure 2: Comparison of the CWBL model and LES results from Porté-Agel et al. for different wind-directions in the Horns Rev windfarm, see the left sketch. The right panels show that, depending on the wind direction, the CWBL model gives significantly improved predictions when compared to the Jensen wake model predictions. Figure based on the results presented in Stevens et al, Wind Energy 2016.
Info: Richard Stevens
Fur further information, corresponding movies, available projects, and vacancies look at: http://stilton.tnw.utwente.nl/people/stevensr/
Researchers: Richard Stevens, Mengqi Zhang
Collaborators: Prof. Charles Meneveau (Johns Hopkins University), Prof. Dennice Gayme (Johns Hopkins University), Michael Wilczek (Max-Planck Institute Gottingen)
Embedding: JMBC
Sponsors: FOM(NWO-ENW),STW
