Multiphase Rayleigh-Bénard convection
Despite the fact that boiling or condensation occur naturally (atmospheric clouds) and in many industrial applications where convection is present (e.g. vapor generators in nuclear power plants, distillers), most studies have focused on single-phase convection. Recent experiments on multiphase Rayleigh-Bénard convection have shown that vapor bubbles dispersed in a liquid or droplets dispersed in a vapor can lead to a dramatic increase in the heat transfer properties of the system (J. Zhong, D. Funfschilling, G. Ahlers, Phys. Rev. Lett. 102, 124501 (2009)). The dispersed phases interacts with the primary phase thermally and mechanically, allowing for the possibility of enhancement or attenuation of global properties like heat transfer and turbulence in the cell.
When phase-change between vapor and liquid is present, a new key parameter is needed to define the system – Ja, the Jakob number, characterizes the ratio of sensible to latent heat associated with the phase change. A Jakob number approaching zero means that the latent heat needed for phase change is diverging, so that a vapor bubble initiated with a certain size, remains that size. As the Jakob number is increased from zero, phase change occurs more readily so that a vapor bubble will grow or shrink rapidly depending on the local thermal environment. As a bubble grows in size, it rises rapidly, driving microscale convection and generating pseudo-turbulence, leading to an overall destabilization of the flow.
We use direct numerical simulations (DNS) to quantitatively explore the effects on the system’s global properties. As shown in Figure 1, the total heat transfer, described by the Nusselt number increases as more bubbles are injected into the cell, and also as the Jakob number is increased.
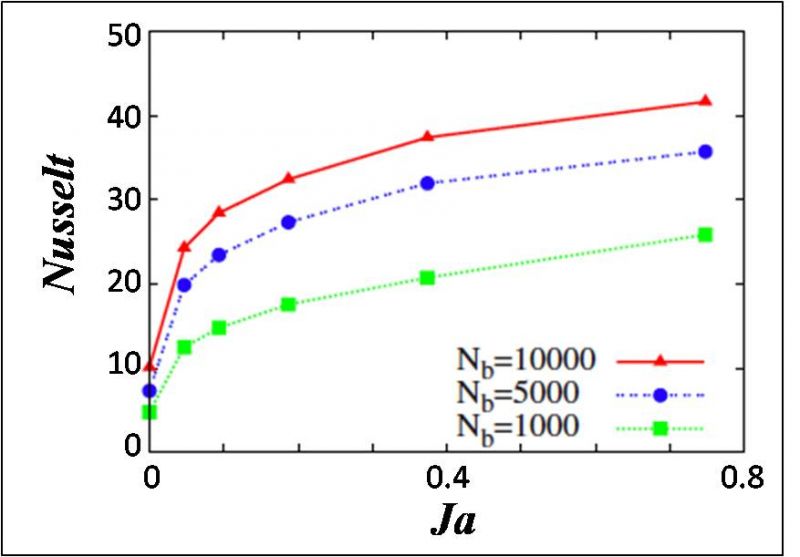
Figure 1: Average Nusselt number of flow as a function of Jakob number, Ja. Bubbles with fixed size at Ja=0 carry heat across the cell, but dampen the flow, and thus the heat transport (via the liquid convection) is not increased. As the Jakob number is increased, the rising motion of the bubbles generates stronger additional flow, enhancing the heat transferred by the liquid phase.
In Figure 2, the Reynolds number of the flow also increases with the number of injected bubbles, except when the Jakob number is very small because in that case the bubbles stabilize the flow by reducing the temperature gradients which drive the flow.
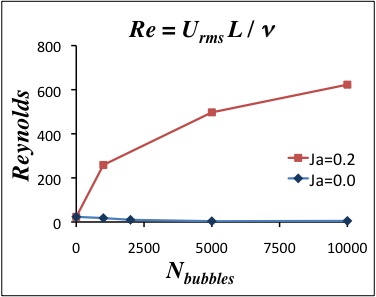
Figure 2: Reynolds number of flow as function of total number of bubbles, calculated from the rms velocity fields. Bubbles with fixed size at Ja=0 dampen the flow by reducing the temperature gradients that cause the liquid to become buoyant. In constrast, the rapidly growing Ja=0.2 bubbles drive the flow as they rise, causing an enhancement of turbulence which is not compensated by the stabilizing thermal effects.
Info: Detlef Lohse
Researchers: Rajaram Lakkaraju, Laura Stricker, Kristján Guðmundsson, Chao Sun, Andrea Prosperetti, Roberto Verzicco, Detlef Lohse.
Collaborators: Federico Toschi (TU Eindhoven), Enrico Calzavarini (Lyon, France), Paolo Oresta (Università del Salento, Italy)
Embedding: JMBC
Sponsors: FOM
